In quantum physics, you can use operators to determine the energy eigenstate of a harmonic oscillator in position space. The charm of using the operators a and
is that given the ground state, | 0 >, those operators let you find all successive energy states. If you want to find an excited state of a harmonic oscillator, you can start with the ground state, | 0 >, and apply the raising operator,
For example, you can do this:
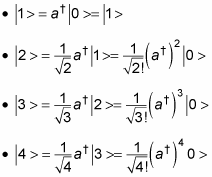
And so on. In general, you have this relation:

Can’t you get a spatial eigenstate of this eigenvector? Something like
not just | 0 >? Yes, you can. In other words, you want to find
So you need the representations of
in position space.
The p operator is defined as
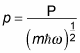
Because
you can write
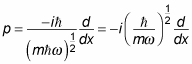
And writing
this becomes
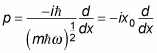
Okay, what about the a operator? You know that
And that
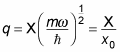
Therefore,
You can also write this equation as
Okay, so that’s a in the position representation. What’s
That turns out to be this:
Now’s the time to be clever. You want to solve for | 0 > in the position space, or x | 0 >. Here’s the clever part — when you use the lowering operator, a, on | 0 >, you have to get 0 because there’s no lower state than the ground state, so a | 0 > = 0. And applying the x | bra gives you x | a | 0 > = 0.
That’s clever because it’s going to give you a homogeneous differential equation (that is, one that equals zero). First, you substitute for a:
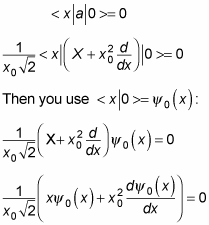
Multiplying both sides by
gives you the following
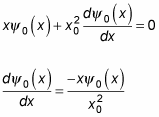
The solution to this compact differential equation is
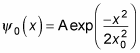
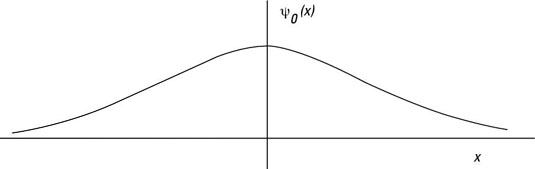
That’s a gaussian function, so the ground state of a quantum mechanical harmonic oscillator is a gaussian curve, as you see in the figure.