In quantum physics, in order to find the second-order corrections to energy levels and wave functions of a perturbed system, En, you need to calculate E(2)n, as well as
So how do you do that? You start with three perturbed equations:
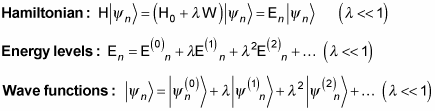
You then combine these three equations to get this jumbo equation:
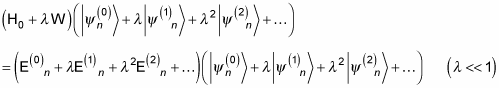
From the jumbo equation, you can then find the second-order corrections to the energy levels and the wave functions. To find E(2)n, multiply both sides of
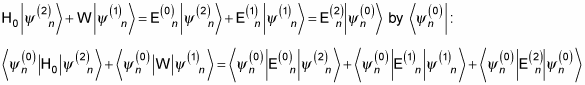
This looks like a tough equation until you realize that
is equal to zero, so you get
Because
is also equal to zero, and again neglecting the first term, you get
E(2)n is just a number, so you have
And of course, because
you have
Note that if
is an eigenstate of W, the second-order correction equals zero.
Okay, so
How can you make that simpler? Well, from using
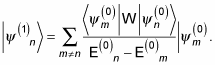
Substituting that equation into
gives you
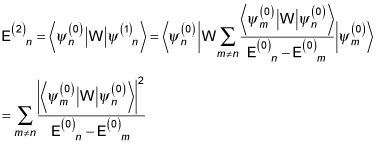
Now you have
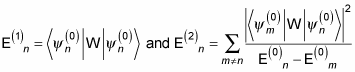
Here's the total energy with the first- and second-order corrections:
So from this equation, you can say
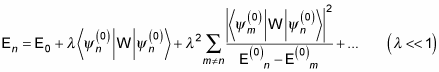
That gives you the first- and second-order corrections to the energy, according to perturbation theory.






