Measuring the Volume of a Pyramid

Suppose that you want to find the volume of a pyramid with a 6-x-6-unit square base and a height of 3 units. Geometry tells you that you can use the following formula:

This formula works just fine, but it doesn’t give you insight into how to solve similar problems; it works only for pyramids. The meat-slicer method, however, provides an approach to the problem that you can generalize to use for many other types of solids.

To start out, you skewer this pyramid on the x-axis of a graph, as shown in the figure. Notice that the vertex of the pyramid is at the origin, and the center of the base is at the point (3, 0).

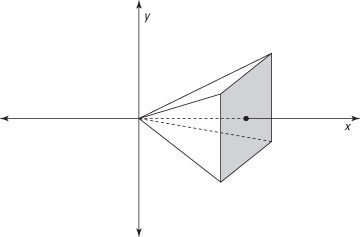
To find the exact volume of the pyramid, here’s what you do:

1. Find an expression that represents the area of a random cross section of the pyramid in terms of x.

   At x = 1, the cross section is 2² = 4. At x = 2, it’s 4² = 16. And at x = 3, it’s 6² = 36. So generally speaking, the area of the cross section is:

   A = (2x)² = 4x²

2. Use this expression to build a definite integral that represents the volume of the pyramid.

   In this case, the limits of integration are 0 and 3, so:

   

3. Evaluate this integral:

   

This is the same answer provided by the formula for the pyramid. But this method can be applied to a far wider variety of solids.