The simplest and most basic trig identities (equations of equivalence) are those involving the reciprocals of the trigonometry functions. To jog your memory, a reciprocal of a number is 1 divided by that number — for example, the reciprocal of 2 is 1/2. Another way to describe reciprocals is to point out that the product of a number and its reciprocal is 1.
The same goes for the trig reciprocals.
Here’s how the reciprocal identities are defined:
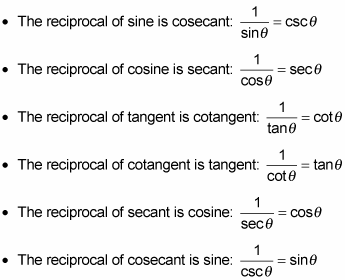
In true fashion, when you multiply the reciprocals together, you get 1:

There’s always the warning, though, that the function can’t be equal to 0; the number 0 doesn’t have a reciprocal. The reciprocal identity is a very useful one when you’re solving trig equations. If you find a way to multiply each side of an equation by a function’s reciprocal, you may be able to reduce some part of the equation to 1 — and simplifying is always a good thing.






