Your quantum physics instructor may ask you to solve for the wave function for a made-up particle of mass m in a hydrogen atom. To do this, you can begin by using a modified Schrödinger equation that solves for large and small r:
Because the Schrödinger equation contains terms involving either R or r but not both, the form of this equation indicates that it’s a separable differential equation. And that means you can look for a solution of the following form:
Substituting the preceding equation into the one before it gives you the following:
And dividing this equation by
gives you
This equation has terms that depend on either
but not both. That means you can separate this equation into two equations, like this (where the total energy, E, equals ER + Er):
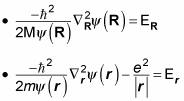
Multiplying
gives you
And multiplying
gives you
Now you can solve for r, both small and large.
Solving for small r
The Schrödinger equation for
is the wave function for a made-up particle of mass m (in practice,
is pretty close to
so the energy, Er, is pretty close to the electron’s energy). Here’s the Schrödinger equation for
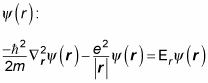
You can break the solution,
into a radial part and an angular part:
The angular part of
is made up of spherical harmonics,
so that part’s okay. Now you have to solve for the radial part, Rnl(r). Here’s what the Schrödinger equation becomes for the radial part:
where
To solve this equation, you take a look at two cases — where r is very small and where r is very large. Putting them together gives you the rough form of the solution.
Solving for large r
For very large r,

Because the electron is in a bound state in the hydrogen atom, E

Note that
diverges as r goes to infinity because of the
term, so B must be equal to zero. That means that





