The double-angle formula for sine comes from using the trig identity for the sine of a sum, sin (α + β) = sinαcosβ + cosαsinβ. If α = β, then you can replace β with α in the formula, giving you
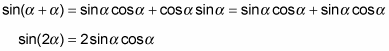
For example, you can use this double-angle identity to find the function value for the sine of 180 degrees.
Determine which angle is half of 180 degrees.
Twice 90 is 180, so the choice is 90 degrees.
Substitute the measure into the double-angle identity for sine.
sin180° = sin 2 (90°) = 2 sin 90° cos 90°
Replace the angles with the function values and simplify the answer.
sin 180° = 2(1)(0) = 0





