You can use the reciprocal of the number that you’re trying to “get rid of” if a fraction is multiplying the variable. You solve linear equations with reciprocals when you see a fraction — it's easier than using multiplication or division.
Here is an example of a fraction multiplying the variable:
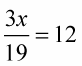
Look at the following examples of reciprocals — after the reciprocals, you can see how each, when multiplied together, equals 1.
5 and 1/5 are reciprocals:
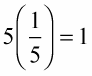
−3/7 and −7/3 are reciprocals:
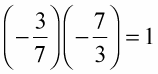
Solving equations in the fewest possible steps is usually preferable.
Example:
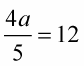
Use the following steps to solve for the variable, using reciprocals.
Multiply each side by the reciprocal.
In this example, the variable is multiplied by 4/5. So each side of the equation needs to be multiplied by the reciprocal 5/4.
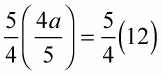
Reduce and simplify.
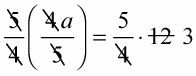
On the left side, the 5s and 4s cancel each other out, and on the right side, 12 divided by 4 equals 3, resulting in:
a = 5 × 3
a = 15
Decimals can be made into fractions, which are much easier to deal with and avoid the problem of inadvertently misplacing the decimal when performing operations.

