Because you spend a ton of time in pre-calculus working with trigonometric functions, you need to understand ratios. One important ratio in right triangles is the sine. The sine of an angle is defined as the ratio of the opposite leg to the hypotenuse. In symbols, you write
Here’s what the ratio looks like:
In order to find the sine of an angle, you must know the lengths of the opposite side and the hypotenuse. You will always be given the lengths of two sides, but if the two sides aren’t the ones you need to find a certain ratio, you can use the Pythagorean theorem to find the missing one. For example, to find the sine of angle F (sin F) in the figure, follow these steps:
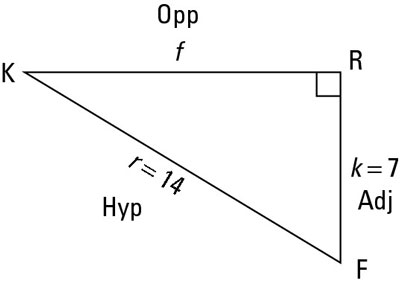
Identify the hypotenuse.
Where’s the right angle? It’s

so side r, across from it, is the hypotenuse. You can label it “Hyp.”
Locate the opposite side.
Look at the angle in question, which is

here. Which side is across from it? Side f is the opposite leg. You can label it “Opp.”
Label the adjacent side.
The only side that’s left, side k, has to be the adjacent leg. You can label it “Adj.”
Locate the two sides that you use in the trig ratio.
Because you are finding the sine of

you need the opposite side and the hypotenuse. For this triangle, (leg)2 + (leg)2 = (hypotenuse)2 becomes f2 + k2 = r2. Plug in what you know to get f2 + 72 = 142. When you solve this for f, you get

Find the sine.
With the information from Step 4, you can find that

which reduces to







