Integration by partial fractions works only with proper rational expressions, but not with improper rational expressions. Telling a proper fraction from an improper one is easy: A fraction a/b is proper if the numerator (disregarding sign) is less than the denominator, and improper otherwise.
With rational expressions, the idea is similar, but instead of comparing the value of the numerator and denominator, you compare their degrees. The degree of a polynomial is its highest power of x.
A rational expression is proper if the degree of the numerator is less than the degree of the denominator, and improper otherwise.
For example, look at these three rational expressions:
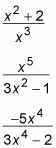
In the first example, the numerator is a second-degree polynomial and the denominator is a third-degree polynomial, so the rational is proper. In the second example, the numerator is a fifth-degree polynomial and the denominator is a second-degree polynomial, so the expression is improper. In the third example, the numerator and denominator are both fourth-degree polynomials, so the rational function is improper.






