An important type of series is called the p-series. A p-series can be either divergent or convergent, depending on its value. It takes the following form:
Here’s a common example of a p-series, when p = 2:
Here are a few other examples of p-series:
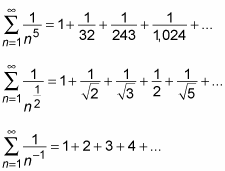
Remember not to confuse p-series with geometric series. Here’s the difference:
A geometric series has the variable n in the exponent — for example,

A p-series has the variable in the base — for example

As with geometric series, a simple rule exists for determining whether a p-series is convergent or divergent.
A p-series converges when p > 1 and diverges when p
Here are a few important examples of p-series that are either convergent or divergent.
When p = 1: the harmonic series
When p = 1, the p-series takes the following form:
This p-series is important enough to have its own name: the harmonic series. The harmonic series is divergent.
When p = 2, p = 3, and p = 4
Here are the p-series when p equals the first few counting numbers greater than 1:
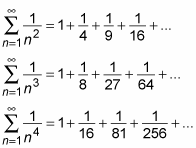
Because p > 1, these series are all convergent.
When p = 1/2
When p = 1/2 the p-series looks like this:
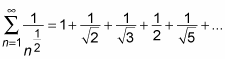
Because p ≤ 1, this series diverges. To see why it diverges, notice that when n is a square number, say n = k2, the nth term equals
So this p-series includes every term in the harmonic series plus many more terms. Because the harmonic series is divergent, this series is also divergent.






