When solving area problems, you sometimes need to split an integral into two separate definite integrals. Here’s a simple but handy rule for doing this that looks complicated but is really very easy:
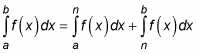
This rule just says that you can split an area into two pieces and then add up the pieces to get the area that you started with.
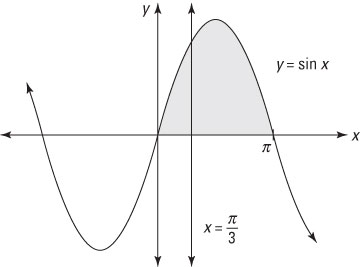
For example, the entire shaded area in the figure is represented by the following integral, which you can evaluate easily:
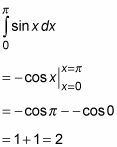
Drawing a vertical line at
and splitting this area into two separate regions results in two separate integrals:
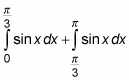
It should come as no great shock that the sum of these two smaller regions equals the entire area:
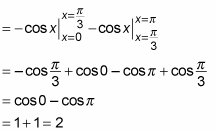
Although this idea is ridiculously simple, splitting an integral into two or more integrals can be a powerful tool for solving a variety of area problems.






