You can use sigma notation to write out the right-rectangle sum for a function. For example, say you’ve got f (x) = x2 + 1.
By the way, you don’t need sigma notation for the math that follows. It’s just a “convenience” — yeah, right. Cross your fingers and hope that your teacher decides not to cover the following. It can get pretty hairy.
Recall the formula for a right sum:
Here’s the same formula written with sigma notation:
Now, work this formula out for the six right rectangles in the figure below.
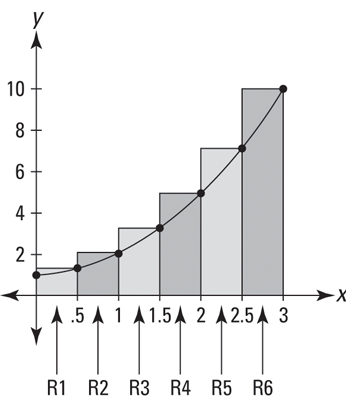
In the figure, six right rectangles approximate the area under
between 0 and 3.

If you plug 1 into i, then 2, then 3, and so on up to 6 and do the math, you get the sum of the areas of the rectangles in the above figure. This sigma notation is just a fancy way of writing the sum of the areas of the six rectangles.






