A kite is a quadrilateral in which two disjoint pairs of consecutive sides are congruent (“disjoint pairs” means that one side can’t be used in both pairs). Check out the kite in the below figure.
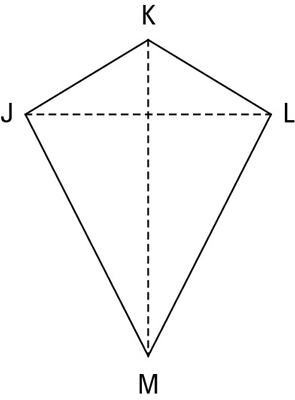
The properties of the kite are as follows:
Two disjoint pairs of consecutive sides are congruent by definition

Note: Disjoint means that the two pairs are totally separate.
The diagonals are perpendicular.
One diagonal (segment KM, the main diagonal) is the perpendicular bisector of the other diagonal (segment JL, the cross diagonal). (The terms “main diagonal” and “cross diagonal” are made up for this example.)
The main diagonal bisects a pair of opposite angles (angle K and angle M).
The opposite angles at the endpoints of the cross diagonal are congruent (angle J and angle L).
The last three properties are called the half properties of the kite.
Grab an energy drink and get ready for another proof.

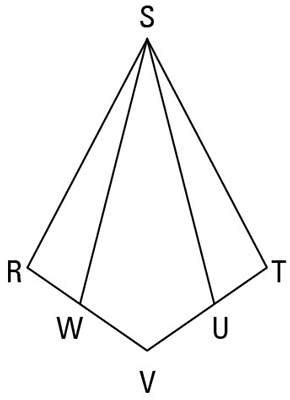
Statement 1:
Reason for statement 1: Given.
Statement 2:
Reason for statement 2: A kite has two disjoint pairs of congruent sides.
Statement 3:
Reason for statement 3: Given.
Statement 4:
Reason for statement 4: If two congruent segments (segment WV and segment UV) are subtracted from two other congruent segments (segment RV and segment TV), then the differences are congruent.
Statement 5:
Reason for statement 5: The angles at the endpoints of the cross diagonal are congruent.
Statement 6:
Reason for statement 6: SAS, or Side-Angle-Side (1, 5, 4).
Statement 7:
Reason for statement 7: CPCTC (Corresponding Parts of Congruent Triangles are Congruent).





