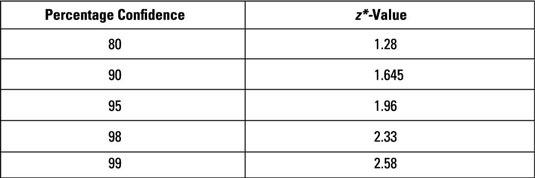
The following table provides the z*- values for selected (percentage) confidence levels.
Sample questions
-
What is the margin of error if the researcher wants to be 99% confident of the result?
Answer: plus/minus $3.72
The formula for margin of error when estimating a population mean is

where z* is the value from the table for a given confidence level (99% in this case, or 2.58),

is the standard deviation ($25), and n is the sample size (300).
Now, substitute the values into the formula and solve:

The margin of error for a 99% confidence interval for the population mean is plus/minus $3.72.
-
What is the margin of error if the researcher wants to be 95% confident in the result?
Answer: plus/minus $2.83
The formula for margin of error when estimating a population mean is

where z* is the value from the table for a given confidence level (95% in this case, or 1.96),

is the standard deviation ($25), and n is the sample size (300).
Now, substitute the values into the formula and solve:

The margin of error for a 95% confidence interval for the population mean is plus/minus $2.83.
-
What is the lower limit of an 80% confidence interval for the population mean, based on this data?
Answer: $83.15
To find the lower limit for the 80% confidence interval, you first have to find the margin of error. The formula for the margin of error when estimating a population mean is

where z* is the value from the table for a given confidence level (80% in this case, or 1.28),

is the standard deviation ($25), and n is the sample size (300).
Now, substitute the values into the formula and solve:

Next, subtract the MOE from the sample mean to find the lower limit: $85.00 – $1.85 = $83.15.






