Navigators, surveyors, and carpenters all use the same angle measures, but the angles start out in different positions or places. In trigonometry and most other mathematical disciplines, you draw angles in a standard, universal position, so that mathematicians around the world are drawing and talking about the same thing.
Positioning initial and terminal sides
An angle in standard position has its vertex at the origin of the coordinate plane. Its initial ray (starting side) lies along the positive x-axis. Its terminal ray (ending side) moves counterclockwise from the initial side.
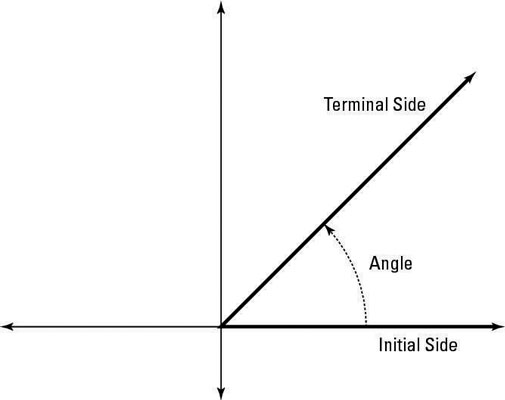
If the terminal ray moves clockwise instead of counterclockwise, then the measure is a negative value. You often name angles in standard position with a Greek letter.
The lengths of the rays that create the angle have nothing to do with the angle size. You can extend rays as long as you need them to be, and the angle measure won’t change. Only the position of the terminal ray determines the angle.
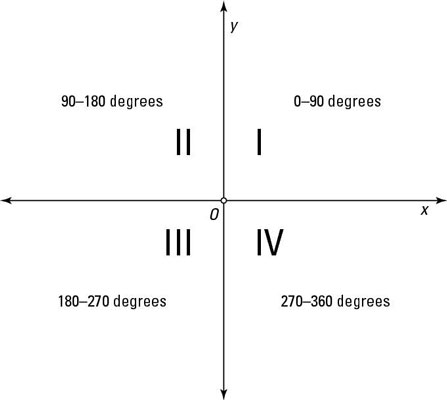
Measuring by quadrants
Angles in the standard position are used in calculus, geometry, trigonometry, and other math subjects as a basis for discussion. Being able to recognize a particular angle by the quadrant its terminal side lies in and, conversely, to know which angles have their terminal sides in a particular quadrant is helpful when working in these areas.
Angles in standard position that measure between 0 and 90 degrees have their terminal sides in Quadrant I. The angles measuring between 90 and 180 degrees have their terminal sides in Quadrant II. Angles measuring between 180 and 270 have their terminal sides in Quadrant III, and those measuring between 270 and 360 have their terminal sides in Quadrant IV.
Angles measuring exactly 90, 180, 270, and 360 degrees do not have a terminal side that lies in a quadrant, and they’re referred to as quadrantal angles.