Some fraternity brothers want to order pizza — and you know how hungry college men can be. The big question is, which has bigger slices of pizza: a 12-inch pizza cut into six slices, or a 15-inch pizza cut into eight slices?
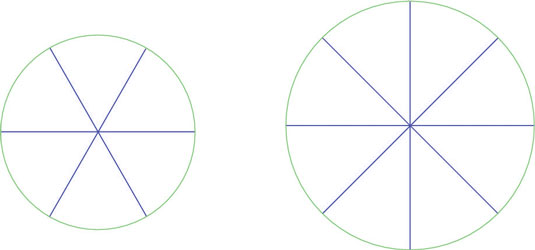
The figure shows a 12-inch pizza and a 15-inch pizza, both of which are sliced. Can you tell by looking at them which slices are bigger — that is, have more area?
The 12-inch pizza is cut into six pieces. Each piece represents an angle of 60 degrees, which is
radians, so you find the area of each sector (slice) by using the formula for the area of a sector using radians and putting the 6 in for the radius of the pizza with a 12-inch diameter. The answer is

The 15-inch pizza is cut into eight pieces. Each piece represents an angle of 45 degrees, which is
radians, so, letting the radius be 7.5 this time, the area of each sector is
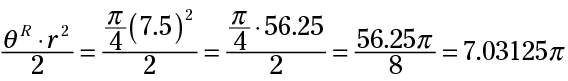
This result doesn’t tell you exactly how many square inches are in each slice, but you can see that a slice of this 15-inch pizza has an area of 7.03125π square inches, and a slice of the 12-inch pizza has an area of 6π square inches. The 15-inch pizza has bigger pieces, even though you cut it into more pieces than the 12-inch pizza. And, by the way, the difference is slightly over three square inches per slice.




