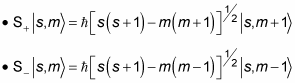How Spin Operators Resemble Angular Momentum Operators

Because spin is a type of built-in angular momentum, spin operators have a lot in common with orbital angular momentum operators. As your quantum physics instructor will tell you, there are analogous spin operators, S² and S_z, to orbital angular momentum operators L² and L_z. However, these operators are just operators; they don’t have a differential form like the orbital angular momentum operators do.

In fact, all the orbital angular momentum operators, such as L_x, L_y, and L_z, have analogs here: S_x, S_y, and S_z. The commutation relations among L_x, L_y, and L_z are the following:

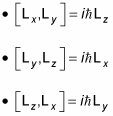
And they work the same way for spin:

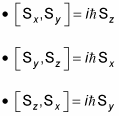
The L² operator gives you the following result when you apply it to an orbital angular momentum eigenstate:

And just as you’d expect, the S² operator works in an analogous fashion:

The L_z operator gives you this result when you apply it to an orbital angular momentum eigenstate:

And by analogy, the S_z operator works this way:

What about the raising and lowering operators, L₊ and L_–? Are there analogs for spin? In angular momentum terms, L₊ and L_– work like this:

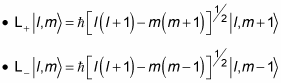
There are spin raising and lowering operators as well, S₊ and S_–, and they work like this: