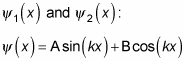Infinite square well, in which the walls go to infinity, is a favorite problem in quantum physics. To solve for the wave function of a particle trapped in an infinite square well, you can simply solve the Schrödinger equation.
Take a look at the infinite square well in the figure.
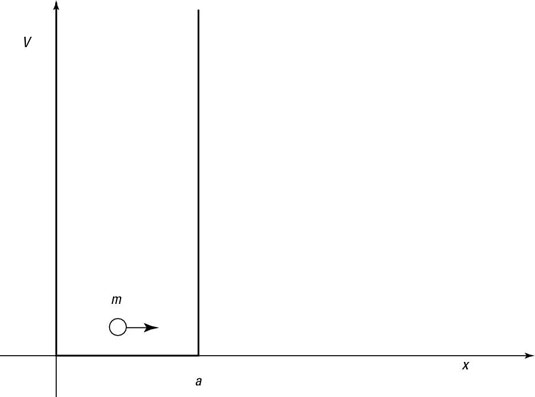
Here’s what that square well looks like:
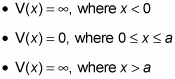
The Schrödinger equation looks like this in three dimensions:
Writing out the Schrödinger equation gives you the following:
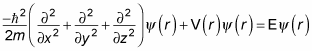
You’re interested in only one dimension — x (distance) — in this instance, so the Schrödinger equation looks like
Because V(x) = 0 inside the well, the equation becomes
And in problems of this sort, the equation is usually written as
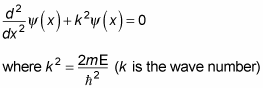
So now you have a second-order differential equation to solve for the wave function of a particle trapped in an infinite square well.
You get two independent solutions because this equation is a second-order differential equation:
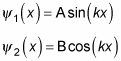
A and B are constants that are yet to be determined.
The general solution of
is the sum of