Power and Energy Signal Classifications

To classify a signal x(t) according to its power and energy properties, you need to determine whether the energy is finite or infinite and whether the power is zero, finite, or infinite. The measurement unit for power and energy are watts (W) and joules (J).

In circuit theory, watts delivered to a resistor of R ohms is represented as

where V is voltage in volts and I is current in amps.

The figure shows that a circuit is composed of resistor and voltage sources, demonstrating the interconnection of signals and systems with physics and circuit concepts. A simple power calculation in circuit analysis becomes instantaneous power with time dependence, and the resistance is normalized to 1 ohm as used in signals and systems terminology.

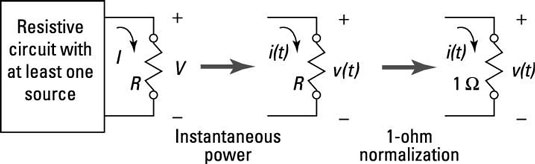
With the circuit calculation of power, you can introduce time dependence and define a signal’s instantaneous power as

Computer and electrical engineers use the abstraction available through mathematics to work in a convenient 1-ohm environment.

The significance of the 1-ohm impedance normalization is that instantaneous power is simply v²(t) or i²(t). It’s convenient then to use x(t) to represent the signal — voltage or current. Keep in mind that, unless told otherwise,

in all signals. When modeling results need to be coupled to physical, real-world measurements, you can add back in the resistance, or impedance level.

Average power, P (watts), and average energy, E (joules), are defined as follows:

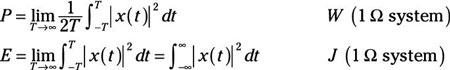
The | |² is used when the signal happens to be complex. For x(t) periodic, you can simplify the average power formula to

where T₀ is the period. Note that the single limit on the far right integral means that you can use any T₀ interval for the calculation. The limit is gone, and the integration now covers just one period.

For x(t) to be a power signal,

and

To understand why this is, think about a signal that has nonzero but finite power. Integrating the power over all time gives you energy. When you integrate nonzero finite power over infinite time, you get infinite energy.

An energy signal requires

and

Yet some signals are neither power nor energy types because they have unbounded power and energy. For these,

Mathematically, a signal can have infinite power, but that’s not a practical reality. Infinite energy indicates that the signal duration is likely infinite, so it doesn’t make sense to deal with energy. Power, on the other hand, is energy per unit time averaged over all time, making power more meaningful than energy.